
A wave of optimism followed. Perhaps, researchers believe, we will be able to invent quantum algorithms that can solve a vast number of different problems.
But progress has stalled. “It’s kind of disappointing,” says Ryan O’Donnell of Carnegie Mellon University. “People will say, ‘This is awesome, I’m sure we’re going to get all sorts of other amazing algorithms,’ and it’s not.” Scientists have only found significant speedups for single, narrow class problems in a standard set called NP, meaning they have efficient verifiable solutions — such as factorization.
This has been the case for the past three years. Then in April, researchers invented a whole new kind of problem that quantum computers should be able to solve faster than classical computers. It involves computing the input of a complex mathematical process based only on its messy output. Whether this problem stands alone or the first of many others remains to be determined.
“There’s a sense of excitement,” says Vinod Vaikuntanathan, a computer scientist at the Massachusetts Institute of Technology. “A lot of people are thinking about what’s out there.”
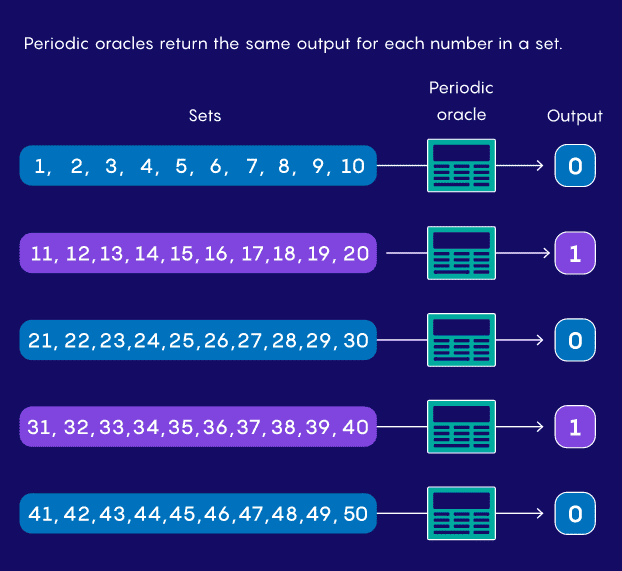
Computer scientists try to understand what quantum computers do better by studying the mathematical models that represent them. Typically, they imagine a model of a quantum or classical computer paired with an ideal computer called an oracle. An oracle is like a simple mathematical function or computer program that takes input and outputs a predetermined output.
They may have random behavior, outputting “yes” if the input is in some random range (for example, 12 to 67) and “no” otherwise. Or they could be periodic, so an input between 1 and 10 returns “yes”, 11 to 20 yields “no”, 21 to 30 yields “yes” again, and so on.
Suppose you have one of these periodic oracles, but you don’t know the period. All you can do is feed it numbers and see what it outputs. Given these constraints, how fast can a computer find cycles? In 1993, Daniel Simon, then at the University of Montreal, discovered that quantum algorithms could compute answers to closely related problems faster than any classical algorithm.
This result allowed Simon to identify one of the first signs of where quantum computers could offer significant advantages. But when he submitted his paper to a major conference, it was rejected. The paper did, however, interest a junior member of the conference program committee, Peter Shor, who was then at Bell Labs in New Jersey.
Shor went on to find that he could tweak Simon’s algorithm to calculate the oracle’s period, if it had one. Then he realized that he could tweak the algorithm again to solve an equation that behaves like a periodic prediction: an equation describing factorization, which is periodic.
Shor’s results are historic. The quantum algorithm he discovered can rapidly reduce huge numbers to their constituent prime factors, something no known classical algorithm can do. In the years that followed, researchers discovered other efficient quantum algorithms. Some of them, like Shor’s algorithm, even offer exponential advantages, but no one has been able to demonstrate a significant quantum advantage on any aperiodic NP problem.
Due to the lack of progress, two computer scientists, Scott Aaronson of the University of Texas at Austin and Andris Ambainis of the University of Latvia, made observations. Proofs of quantum superiority always seem to rely on predictions with some non-random structure, such as periodicity. In 2009, they speculated that there would be no significant speedup for random or unstructured NP problems; no exception could be found.
Their conjecture limits the capabilities of quantum computers. But it only says that for certain types of unstructured NP problems – those that answer yes or no – there is no significant speedup. If a problem involves finding a more specific, quantitative answer, a so-called search problem, then this conjecture does not apply.
With this in mind, researchers at NTT’s Social Informatics Laboratory, Takashi Yamakawa, and Mark Zhandry at NTT Research and Princeton University decided to experiment with a specific search problem posed by Oded Regev in 2005.
Imagine a set of weather vanes all pointing in the same direction. Give each of them a measured push and let the gust of wind affect their direction. Regev wants to determine where they initially pointed based on their final orientation. Problems like this came to be known as “mislearning” because thrust and wind act like random sources of error in the original direction. There is evidence that both classical and quantum algorithms are difficult to solve.
Yamakawa and Zhandry tweaked the settings. They modified these starting forces to make them more predictable. They also made the wind determined by a random oracle, so it was even more random in some cases, but completely dormant in others.
With these modifications, the researchers found that quantum algorithms can efficiently find the initial orientation. They also proved that any classical algorithm must be exponentially slower. Like Shor, they then tweaked the algorithm to solve a realistic version of the problem, replacing the prophecy with an actual mathematical equation.
Computer scientists are still trying to understand and solve this problem. Vaikuntanathan compares this to a different situation that arises when doing data compression: when information is compressed, two bits can accidentally squeeze into the same place, overwriting them. The problem of predicting these collisions in advance in order to avoid them has some similarities. “It’s a class of problems that basically look like this,” he said. “Maybe these problems can be solved quantum.”
The hope is that unstructured problems like new problems can be solved even on today’s fledgling versions of quantum computers, providing a way to test them. The thinking at the time was that unstructured problems might require fewer resources to program or be less sensitive to noise because they are already random. But so far, this new problem still seems too advanced for existing quantum computers to solve. “It was a weird question. I didn’t think about defining it,” Aaronson said, “but in retrospect, it had some really nice features.”
This result provides the first example of a significant quantum advantage on an unstructured NP problem. Will there be many other problems in the quantum world that go from almost unsolvable to solvable? Now there are even more reasons to think so.
“It kind of upends our view of what problems quantum computers are good at solving,” O’Donnell said.




GIPHY App Key not set. Please check settings